|
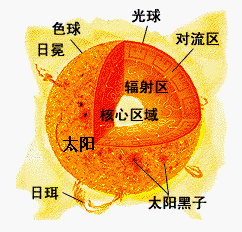
光 球
photosphere
太阳大气最低的一层,即一般用白光所观测到的太阳表面
[厚度仅500公里左右]
。我们接收到的太阳能量基本上是光球发出的。因此,太阳的光谱实际上就是光球的光谱。
*太阳黑子*
*光斑*
*米粒组织*
*超米粒组织*
物理状态
虽然整个说来光球是明亮的,但各部分亮度却很不均匀。在非扰光球中布满米粒组织,估计总数达到400万颗。在光球的活动区,有太阳黑子、光斑,偶尔还有白光耀斑。它们的亮度、物理状态和结构都相差悬殊。平均的非扰光球上每平方厘米每秒发出的辐射流量为6.3X10
尔格,由此可算出光球的有效温度为5500度。这一辐射流量是各波段辐射强度的总和。光球的温度随高度而不同,从内部向外,温度逐渐降低。在光球与色球的交界处,温度降到最低值,只有4000多度,但接着又逆升,在日冕中竟高达上百万度。光球的物质密度约为每立方厘米10克,气体压力大致等于10达因/厘米。
化学成分
通过太阳光谱线的证认,可以定性地知道太阳上有哪些化学元素,但还应定量地测出太阳上各种元素的含量。
- 定量研究的经典方法是生长曲线法。这条曲线表示某一元素的谱线的等值宽度与产生该谱线起始跃迁能态的原子数之间的关系。在已知生长曲线的情况下,只须由观测的谱线轮廓求出等值宽度,便可得到相应的原子数。由同一元素的若干条谱线求得一系列相应的原子数,从而求和得出该元素的原子总数。对一系列元素进行这样的工作,便可测定太阳的化学成分。
- 有一种新的方法是光谱综合法。它的主要内容是采用包括化学含量在内的一系列物理参数,计算一定波长范围内所有谱线的轮廓,并与观测进行对比,如果不尽符合,就调整化学含量或其它参数,直到比较符合为止。
下表列出了光球中各种元素的相对含量A的常用对数。表中没有列出氦的含量,因为光球光谱中没有氦线。但通过色球和日珥的光谱研究,得出氦和氢的含量比为63:1000。太阳大气各层由于经常处于运动状态,化学成分应当基本一致。因此,这个数字也可代表光球的氦含量。
太阳光球的化学成分
|
原子序数
|
元素
|
lgA
|
原子序数
|
元素
|
lgA
|
|
1
|
H
|
0.00
|
41
|
Nb
|
-9.70
|
|
3
|
Li
|
-11.40
|
42
|
Mo
|
-10.10
|
|
4
|
Be
|
-10.94
|
44
|
Ru
|
-10.43
|
|
5
|
B
|
-9.20
|
45
|
Rh
|
-10.45
|
|
6
|
C
|
-3.43
|
46
|
Pd
|
-10.43
|
|
7
|
N
|
-3.94
|
47
|
Ag
|
-11.33
|
|
8
|
O
|
-3.17
|
48
|
Cd
|
-10.03
|
|
9
|
F
|
-7.44
|
49
|
In
|
-10.29
|
|
10
|
Ne
|
-4.55
|
50
|
Sn
|
-10.29
|
|
11
|
Na
|
-5.76
|
51
|
Sb
|
-11.25
|
|
12
|
Mg
|
-4.46
|
55
|
Cs
|
-10.21
|
|
13
|
Al
|
-5.60
|
56
|
Ba
|
-10.20
|
|
14
|
Si
|
-4.45
|
57
|
La
|
-10.19
|
|
15
|
P
|
-6.57
|
58
|
Ce
|
-10.36
|
|
16
|
S
|
-4.79
|
59
|
Pr
|
-10.37
|
|
17
|
Cl
|
-6.35
|
60
|
Nd
|
-10.18
|
|
18
|
Ar
|
-5.27
|
62
|
Sm
|
-10.34
|
|
19
|
K
|
-6.95
|
63
|
Eu
|
-11.51
|
|
20
|
Ca
|
-5.67
|
64
|
Gd
|
-10.88
|
|
21
|
Sc
|
-8.93
|
66
|
Dy
|
-10.89
|
|
22
|
Ti
|
-7.26
|
68
|
Er
|
-11.24
|
|
23
|
V
|
-7.90
|
69
|
Tm
|
-11.57
|
|
24
|
Cr
|
-6.30
|
70
|
Yb
|
-11.19
|
|
25
|
Mn
|
-6.80
|
71
|
Lu
|
-11.16
|
|
26
|
Fe
|
-4.60
|
74
|
W
|
-9.43
|
|
27
|
Co
|
-7.50
|
76
|
Os
|
-11.25
|
|
28
|
Ni
|
-5.72
|
77
|
Ir
|
-9.79
|
|
29
|
Cu
|
-7.55
|
79
|
Au
|
-11.68
|
|
30
|
Zn
|
-7.58
|
80
|
Hg
|
-9.00
|
|
31
|
Ga
|
-9.16
|
81
|
Tl
|
-11.80
|
|
32
|
Ge
|
-8.68
|
82
|
Pb
|
-10.13
|
|
37
|
Rb
|
-9.37
|
83
|
Bi
|
-11.20
|
|
38
|
Sr
|
-9.18
|
90
|
Th
|
-11.18
|
|
39
|
Y
|
-10.38
|
92
|
U
|
-11.40
|
结构模型
光球各处的温度、压力、密度等物理参数都不相等,因而呈现出一定的结构。由于实际情况十分复杂,我们只能在一系列简化假设下建立光球的结构模型。常用的假设是:
|